Some time ago I stumbled upon a paper describing the Tsetlin Machine, a new and interesting machine learning algorithm leveraging binary clause learning as its basic block of operations.

This piqued my interest but and I left the paper for later. Recently I had the occasion to delve into it further and implement it in scala.

Tsetlin Machine

At a very high level a Tsetlin machine is an ensemble learning algorithm for the classification of binary vectors.

The basic block of the Tsetlin machine is a Tsetlin automaton - a simple finite state machine.

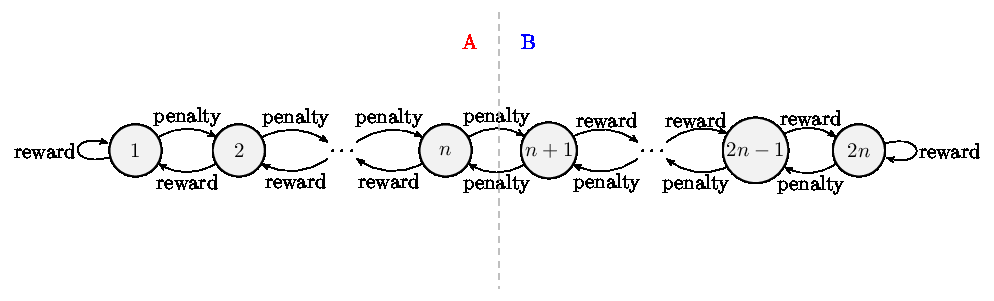
The automaton learns to recognize two actions (labeled A and B on the picture above) while flipping between some given set of \(2n\) states via a mechanism of rewards and penalties. If the automaton is in the first \(n\) states it recognizes the first action (A on the picture obove), while the other \(n\) states recognize the second action (B). Being rewarded in tany state shifts the state of the automaton further from the middle. Given a big enough \(n\) and exposure to training data the automaton would learn the optimal arm for the two armed bandit problem.

The individual automata of the Tsetlin Machine are grouped into teams which learn to detect the presence (active action) or absence of a single bit (inactive action). Half the automata in the team detect the presence of 1s and the other 0s. In effect, a team is a conjunctive clause: a set of terms of expected bit patterns (also known as literals) that matches a portion the input pattern. Since the clause is conjunctive even a single false term negates the entire clause.

For example the clause \(C\) below will be true iff the literals \(x_1\) and \(x_7\) will be true and \(x_2\) will be false. The clause is neutral to all other bit patterns in \(x \in \{0,1\}^d\) where \(d\) is the dimensionality of the classification problem (e.g. in the MNIST classification problem \(d = 28 \cdot 28 = 784\) if we binarized each pixel to 1 bit)¹

The amount of teams in a class is a hyper-parameter and half of the teams in each class predicts if an input vector is a member of the class (I’ll referer to them as positive clauses), and the other half predicts if an input vector is not a member of the class (negative clauses).

The prediction is made on the basis of majority voting:

// scala-like psuedocode
def classify(x: BinaryVector): Int = {
  predictions(x).map { case (class, output) =>
    output.positiveVotes - output.negativeVotes
    cls -> sum
  }.maxBy(_._2)._1
}

Clause Learning

Learning in tsetlin machines is accomplished by (stochastic) feedback - during training each clause gets evaluated on the input vector and randomly selected clauses get feedback. The probability that a clause gets feedback is controlled by a hyper-parameter \(T\) (threshold) in relation to the sum of positive/negative votes.

Where \(v = min(max(-T, \text{vote_sum}), T)\) i.e. the sum gets clipped to \([-T, T]\).

In addition to generating feedback to the class from the training input a second class will be chosen randomly and used as a counterexample.

The probability that an automaton gets feedback is controlled by another hyper-parameter \(s\).

Type I Feedback: Reduce False Negatives

• If a positive clause matches the input and the input belongs to the appropriate class then random automata of the clause that match the input get reinforced. \(P(Reward) = \frac{s-1}{s}\)²
• If a positive clause doesn’t match the input and the input belongs to the appropriate class then random bits of the automata will be penalized probability \(P(Penalty) = \frac{1}{s}\)
• If a negative clause matches the input and the input doesn’t belong to the appropriate clause random automata of the clause that match the input get get reinforced. \(P(Reward) = \frac{s-1}{s}\)³
• If a negative clause doesn’t match the input and the input doesn’t belongs to the appropriate class then random bits of the automata will be penalized probability \(P(Penalty) = \frac{1}{s}\)

Type II feedback: Reduce False Positives

• If a positive clause matches the input and the input doesn’t belong to the appropriate class random automata of the clause get penalized \(P(Penalty) = 1\)

• If a negative clause matches the the input and the input belongs to to the appropriate clause random automata of the clause get penalized \(P(Penalty) = 1\)

Further details of the Tsetlin Machine classification algorithm can be found in the paper.

Implementation

Initially, I based my implementation on the official python implementation of the tsetlin machine.

I created value classes for individual automata:

class Automaton(val value: Int) extends AnyVal {
  def action(implicit desc: Description): Boolean = {
           
    //     negative      positive
    // [ ]  [ ] ... [ ] | [ ] [ ] ... 
    //  \....   ....../   \....   ...'
    //       'v'               'v'
    //      nStates           nStates
    //
    value >= desc.nStates
  }

  def nextStateExclude: Automaton = {
    if (value - 1 >= 0) new Automaton(value - 1) else this
  }

  def nextStateInclude(implicit desc: Description): Automaton = {
    if (value + 1 <= desc.nStates * 2) {
      Automaton(value + 1)
    } else {
      this
    }
  }
}
object Automaton {
  def apply(i: Int): Automaton = new Automaton(i)
}

each automaton was backed by a single Int value stored in an Array[Int] which represented either positive or negative clauses of a class. Since Scala doesn’t play well with collections of value classes yet that was the best I could manage.

Class feedback was stored in:

case class ClassFeedback(positive: Array[Feedback], negative: Array[Feedback])

created fresh for every example.

The python code was of great help when implementing as it dispelled some doubts wrt to the paper.

Performance

Initially I represented the inputs in Array[Boolean] but that turned out to not be viable - the amount of memory needed barely fitted inside 32Gbs so I quickly implemented a BitVector abstraction - packing individual bits into Ints stored as an Array[Int]. I decided not to go with any BitSet implementation just to be sure to use bitcount jvm intrinsic. The intrinsinc didn’t turn out to be that important to overall performance but direct access to the underlying Ints turned out to be a big deal.

Next I looked at the performance - a single iteration on the MNIST data set took about 260-300s or about 100-110 ops/s. Compared to the official C implementation which took 30s or 1000 op/s it was atrocious.

An easy fix was to use parallelism.

Compared to C spawning worker threads is pretty easy - the only thing I needed to implement was synchronizing on the currently updated class and wrapping ThreadSafeRandom. This bumped the amount of ops to 330 - 340, three times worse than C.

Bit based representation.

The tsetlin machine paper mentions a bit based implementation which I wanted to explore next. I didn’t quite get how the testlin machine would work like but looking at the C implementation was of some help.

Instead of storing individual tsetlin automata in an Int the bit based representation jointly represents the state of 32 automata in an Array[Int]. The first Int representing the 32 highest⁴ bits of the tsetlin automata and the next bits reprsenting the lower bits.

This requires implementing increment and decrement operations for the tsetlin automata with respect to some mask.

The tricky part in implementing the bit based implementation was understanding that the machine can no longer be thought as being backed by arbitrary tsetlin automata - only testlin automata which have exactly \(2^N, N \in \mathbb{N}\) states.

I initially tried representing the state jointly as a BitVector but since the increment and decrement operations can finish early depending on the contents of the carry I quickly abandoned this idea and worked on arrays directly.

The authors of the C implementation also implemented some tricks which I deemed unnecessary for my implementation:

• the input (training) vectors \(x_i\) were extended by the negated state of the vector - I wasn’t sure if the cost of shuffling more memory around wouldn’t be washed out by not having to negate it input vector⁵
• the bits of the positive and negative clauses are intertwined in a single array. In essence the even bits always go to the bits of the positive clauses and odd bits to the negative clauses.⁶

I decided to opt out of that and kept positive/negative clauses and positive/negative tsetlin automata separate.

Low level optimizations

At this point I also reduced a lot of unnecessary overhead.

Instead of value classes I used primitives directly - looking at the emitted bytecode Scala 3 doesn’t seem to respect extends AnyVal as the emitted bytecode boxed primitives everywhere. I also ditched the feedback and clause output ADTs in favor of using raw Bytes and Ints. In such tight loops comparing primitives directly made a considerable difference in perfomrmance.

A big problem was the amount of generated garbage - most of it was due to creating arrays of class feedback and clause output - to fix it instead of creating new arrays for I stored them inside a Workspace data structure (aka: poor man’s stack memory).

case class Workspace(
  clauseOutputPositive: BitVector,
  clauseOutputNegative: BitVector,
  positiveFeedback: Array[Byte],
  negativeFeedback: Array[Byte])

Since we already synchronized on the updated class I just created Workspaces for each class.

Another source of garbage was iterating over ranges. Instead of loops like (0 until nDimensions).foreach I was forced to rewrite them to while loops.

Fortunately, I didn’t have to remove all of the generated garbage - only the ones generated in hot loops. And after resolving those three problems the profiler confirmed that the memory usage was stable.

Another strange behavior in Scala 3.0 is that accessing array fields always delegates to a method. I couldn’t find a way to inline them so as a workaround I always stored the array in a local variable. This made a lot of difference in performance.

Inside of the tsetlin machine clause state I moved from a representation of Array[Array[Int]] for the state of the tsetlin automata to Array[Int].

Another hot spot was generating random numbers - fortunately I knew the calls were mostly in the form of 1/s < rand.nextDouble() so I could precompute them.

The last thing I tried was “tactical”⁷ adding of the inline keyword⁸ to a couple of method definitions.

Even with all of those optimizations, I was still behind - for the single threaded implementation this version turned out to a little above 600 ops/s - 60% speed of the C version. On the bright side, the multithreaded implementation was over twice as fast as the C one - with almost 2500 ops/s.

Vectorization

I decided to look at the assembly for the C implementation and just as I thought:

    2324:       66 0f ef c2             pxor   %xmm2,%xmm0
    2328:       66 0f db c8             pand   %xmm0,%xmm1
    232c:       66 0f db c6             pand   %xmm6,%xmm0
    2330:       0f 11 02                movups %xmm0,(%rdx)
    2333:       0f 11 4a 10             movups %xmm1,0x10(%rdx)

the C compiler was able to optimize the for loops into vectorized code. I was never going to be able to achieve comparable performance unless I also used SIMD.

I remembered the last time I had to use JNI and how slow each call outside of the JVM was. The JNI tax is really prohibitable and calling out to native call inside of hot loops would incur performance hits. My alternatives were:

1. Don’t worry about the JNI tax and just call vectorized versions of each instruction.
2. Try to implement as much as possible in native code.

Scala Native

Since the first the first option wasn’t too appealing and calling out to as much native code as possible wasn’t much better than just reimplementing everything in another language I started reading up on scala native.

Recently (January 2022) scala native hit a new milestone and was the first version to support Scala 3.0.

I was pretty excited - the ability to call out to C code without any performance penalties and declare structs would solve a lot of my performance head aches.

Unfortunately, scala-native turned out to be a dead end.

Although scala-native can compile and run single threaded Scala 3.0 code the performance penalty was ridiculous - the code barely ran 1 update operation per second. I hoped this was just because wrapping everything in objects wasn’t the way to go - but rewriting the code to use Ptr[CInt] it jumped to 6 ops/s.

jdk.incubator.vector

Fortunately I remembered that newest jdk was going to include “some” vector API. After looking around a bit it turned out that even jdk 16 included the vector api incubator as does jdk 17. After downloading jdk 17 and adding --add-modules=jdk.incubator.vector to .jvmopts I was able to import jdk.incubator.vector._

I knew nothing about the vector api and I thought there would be a lot of SSE intrinsics I would have to remember - but watching oracle’s vector api introduction and referencing the official java docs was more than enough to get me up to speed for java’s vector api.

Instead of programming with vector intrinsic directly like in C, or writing code with high hopes that it somehow gets vectorized - the java vector api goes the middle road: it provides factory methods for creating vectors of given size (called lanes in the java api) and operations on them. Vectors are stack allocated so they don’t produce any garbage and most instructions on them are inlined.

Operations on vectors are as easy as fetching a chunk of memory from an Array into a vector via:

IntVector.fromArray(IntVectorSpecies, underlying, offset)

IntVectorSpecies is declared as val IntVectorSpecies = IntVector.SPECIES_PREFERRED - which the java vector api defines as the fastest implementation possible.

Storing ints back into an Array can be done via:

bits.intoArray(underlying, offset)

Performing and operation on all Ints in a vector (producing another vector):

nextCarry = bits.and(carry)

The “worst” case is performing lanewise operations which are not defined directly on vectors like this:

bits.lanewise(VectorOperators.XOR, carry) 

Rewriting the code to use SIMD was pretty straightforward. Since I already had everything rewritten to while loops and iterated over arrays directly it only meant taking code like:

while (i < size) {
  val whichBits = xs(i)

  // if (x(k)) actionIncludeReinforceInclude --{
  normal.incBitsInt(i, whichBits)
  // }---
    
  // if (!x(k)) actionIncludeNegatedReinforceInclude --{
  negated.incBitsInt(i, ~whichBits)
  // }---
  
  // if x(k) actionIncludeNegatedReinforceExclude --{
  negated.decBitsInt(i, stream1overS.sample(random) &  whichBits)
  // }---

  // if (!x(k)) actionIncludeReinforceExclude --{
  normal.decBitsInt(i, stream1overS.sample(random) & ~whichBits)
  // }---
  
  i += 1
}

and adding code in the form:

val bound = IntVectorSpecies.loopBound(size)

while (i < bound) {
  val whichBits = IntVector.fromArray(IntVectorSpecies, xs, i)

  // if (x(k)) actionIncludeReinforceInclude --{
  normal.incBitsVec(i, whichBits)
  // }---
    
  // if (!x(k)) actionIncludeNegatedReinforceInclude --{
  negated.incBitsVec(i, whichBits.not)
  // }---
  
  // if x(k) actionIncludeNegatedReinforceExclude --{
  negated.decBitsVec(i, whichBits.and(stream1overS.sampleVec(random)))
  // }---

  // if (!x(k)) actionIncludeReinforceExclude --{
  normal.decBitsVec(i, stream1overS.sampleVec(random).and(whichBits.not))
  // }---
  
  i += IntVectorSpecies.length
}

The loopBound takes care of the fact that vector instructions work on multiple Ints at a time and that multiple sometimes don’t align with the underlying array size.

The definitions of incBitsVec or decBitsVec don’t stray far from their unvectorized implementations.

With hand written vectorized code the single threaded implementation finally beat the C based implementation - 1300 ops/s compared to 1000 op/s and the parallel implementation is almost 4.5 times as fast as the C version.

Closing Thoughts

While writing high perfomring scala code isn’t exactly pleasant, with a lot of diligence and sweat scala code can beat C code.⁹ At the moment the most painful optimizations could in theory even be done by the compiler (i.e. by not boxing extends AnyVal, inlining array acces, and having more control over the memory layout).

Another possible optimization that I didn’t bother checking is aiming for more memory locality in the inc/dec operators. Instead of storing all \(|x|\) highest bits in the first Ints of an array contiguously we could store the most significant bits of the \(8 \cdot 32\) bits (or as many as IntVectorSpecies.length) then \(8 \cdot 32\) lower bits in the next 8 Ints, so on until the \(8 \cdot 32\) least significant bits and then back again to the \(32 \cdot 8\) most significant bits of the next \(32 \cdot 8\) tsetlin automata. This could increase memory locality during training due to the fact that inc/dec operations would work on neighboring memory locations.

While browsing thorugh related Tsetlin machine papers I also found two possible optimizations:

1. asynchronous updates for clauses as described in https://arxiv.org/pdf/2009.04861.pdf
2. indexing clauses as described by https://arxiv.org/abs/2004.03188

Both of which could be easily added to this scala implementation. The second one was particularly interesting as it remedied me of indexing the supports in the AC-* family of algorithms which led me to think if SAT-solving tsetlin machines wouldn’t be possible?¹⁰

The java vector api is turning out to be an excellent addition to the JVM and with further upgrades from Project Panama writing high performance Java could easily be easier than any other language. I’m really positively surprised at the high quality of improvements seen in most recent JVM releases.

Footnotes