Bartosz Witkowski - Blog.
Home About me

Recently I watched In Our Prime a fun 2022 Korean movie which might be summarized as Finding Forrester but With Mathematics.

The protagonist Ji-woo (played by Kim Dong-Hwi) is mentored by Lee Hak-Sung (played by Choi Min-Sik) in mathematics. The way he teaches him doesn’t fit the standard educational cirriculum but is both rigorous and playful in a way that Paul Lockhart would approve¹

In one particular scene (referenced in the trailer) after Lee Hak-Sung does’t manage to awe Ji-woo with Euler’s Identity he tries tying maths to music: by playing the digits of pi:

And that’s neat but do the digits in pi really form a pleasing melody? And if yes how does it work?

I’ll try to find out using my limited understanding of music theory and some understanding of both scala and music theory is needed to follow along.

Did the film makers lie?

If we look at the spectrogram of the song²:

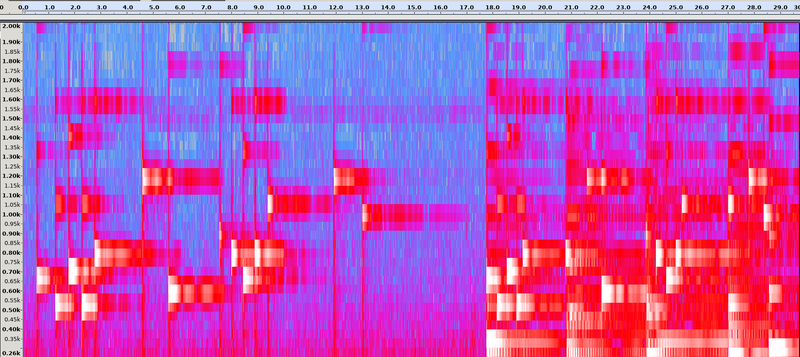Spectogram of the song. The high (white) areas are fundamental frequencies while the lower ones (red) are harmonics.

We can see that the notes might plausible follow the orders of the digits in pi as they cluster around something that could be plausible 1-5 (from 3.1415) and than a jump to 9. But this becomes especially visible if we look at note frequencies and annotate the spectogram with the pitches.

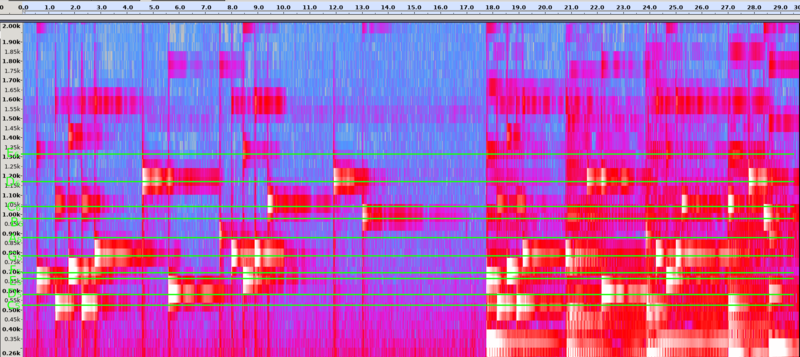Note frequencies annotated on the spectogram

If we note down all the notes from the annotated spectogram we can see they match perfectly to the digits of pi:

E₅	C₅	F₅	C₅	G₅	D₆	A₅	G₅	E₅	G₅	C₆	D₆	B₅
3	1	4	1	5	9	2	6	5	3	5	8	9

Why does it work?

So if it works what’s going on? Is π special? Not really!

If we used any random sequence of digits with the same encoding (C=1, D=2 etc) we would get a similarly pleasing result.

The trick here is that we limit ourselves to the major scale³. Confining ourselves to notes in the major scale will at the very least suggest a tonality. A particular melody (by which I mean the arrangement of the highest voice) along with an underlying harmony (by which I mean the arrangement of lower voices) might also imply a mode or a major/minor key.

Let’s give it a try. If we use java music as a dependency⁴ we can easily generate the notes in scala (3.0)

type Digit = 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9

import jm.music.data.Note 
import jm.constants.Durations

def digitToNoteMajor(d: Digit): Note = {
  val delta = d match {
    case 0 => /* B */  -1 
    case 1 => /* C */  0
    case 2 => /* D */  2
    case 3 => /* E */  4
    case 4 => /* F */  5
    case 5 => /* G */  7
    case 6 => /* A */  9
    case 7 => /* B */  11
    case 8 => /* C */  12
    case 9 => /* D */  14
  }

  // middle C is 60 and each number from 60 is it's difference in semitones.
  val n: Int = delta + (60 + 12)

  new Note(n, Durations.QUARTER_NOTE)
}

We’ll also need a way to write notes as a midi file. We can do this using this function:

import jm.util.Write;
import jm.music.data.Part
import jm.music.data.Score

def renderDigits(
    fileName: String,
    digits: List[Digit],
    d2n: Digit => Note): Unit = {
  val notes = digits.map(digitToNote)

  val part = new Part("part", 0, Part.DEFAULT_CHANNEL)
  val phrase = new jm.music.data.Phrase(notes.toArray)
  part.addPhrase(phrase)

  val score = new Score
  score.setTempo(120)
  score.addPart(part)

  Write.midi(score, fileName)
}

Now calling the code:

val PiDigits: List[Digit] = List(
  3, 1, 4, 1, 5, 9, 2, 6, 5, 3, 5, 8, 9, 7, 9, 3, 2, 3, 8, 4, 6)

val EDigits: List[Digit] = List(
  2, 7, 1, 8, 2, 8, 1, 8, 2, 8, 4, 5, 9, 0, 4, 5, 2, 3, 5, 3, 6)

renderDigits("pi-major.mid", PiDigits, digitToNotePentatonic)
renderDigits("e-major.mid", EDigits, digitToNotePentatonic)

We can listen to the examples:

The example melodies sound pleasing enough but because they end in a completely random place (I picked 20 “just because”) the effect sounds jarring. If we extend the notes to end on a C the effect would be much better.

Here the examples again with more digits (until we find a 1):

val PiDigits: List[Digit] = List(
  3, 1, 4, 1, 5, 9, 2, 6, 5, 3, 5, 8, 9, 7, 9, 3, 2, 3, 8, 4, 6, 2, 6, 4, 
  3, 3, 8, 3, 2, 7, 9, 5, 0, 2, 8, 8, 4, 1)

val EDigits: List[Digit] = List(
  2, 7, 1, 8, 2, 8, 1, 8, 2, 8, 4, 5, 9, 0, 4, 5, 2, 3, 5, 3, 6, 0, 2, 8,
  7, 4, 7, 1)

We can make the melody be more interesting by holding more consonant notes longer and speeding past the dissonant notes. In a major scale nothing will be really dissonant except the major seven but the only true constant notes will be C, F, G - C and its perfect fourth/fifth.

def digitToNote(d: Digit): Note = {
  val (duration, delta) = d match {
    case 0 => /* B MINOR_SECOND   */ Durations.SIXTEENTH_NOTE -> -1 
    case 1 => /* C UNISON         */ Durations.QUARTER_NOTE   -> 0
    case 2 => /* D MAJOR_SECOND   */ Durations.EIGHTH_NOTE    -> 2
    case 3 => /* E MAJOR_THIRD    */ Durations.QUARTER_NOTE    ->4
    case 4 => /* F PERFECT_FOURTH */ Durations.QUARTER_NOTE   -> 5
    case 5 => /* G PERFECT_FIFTH  */ Durations.QUARTER_NOTE   -> 7
    case 6 => /* A MAJOR_SIXTH    */ Durations.EIGHTH_NOTE    -> 9
    case 7 => /* B MAJOR_SIXTH    */ Durations.SIXTEENTH_NOTE -> 11
    case 8 => /* C OCTAVE         */ Durations.QUARTER_NOTE   -> 12
    case 9 => /* D OCTAVE+M2      */ Durations.EIGHTH_NOTE    -> 14
  }

  val n: Int = delta + (60 + 12)

  new Note(n, duration)
}

The result:

To ground the melody further we can add a simple accompaniment. We will just play the Cmaj7 chord but to make it a little bit more interesting every other bar will start with a quarter rest.

import jm.music.data.Phrase
def accompany(
  duration: Double): Phrase = {

  import jm.constants.Pitches._

  val Cmaj7 = Array(c3, e3, g3, b3)

  val phrase = new Phrase(4)

  val rest = new jm.music.data.Rest(Durations.QUARTER_NOTE)

  var cur = 4.0
  while (cur <= (duration - 2 * Durations.WHOLE_NOTE)) {
    phrase.addChord(Cmaj7, Durations.WHOLE_NOTE)
    phrase.addRest(rest)
    phrase.addChord(Cmaj7, Durations.HALF_NOTE + Durations.QUARTER_NOTE)

    cur += 2 * Durations.WHOLE_NOTE
  }

  phrase.setDynamic(jm.constants.Volumes.MP)
  phrase
}

def renderDigitsWithAccompaniament(
    fileName: String,
    digits: List[Digit],
    d2n: Digit => Note): Unit = {
  val notes = digits.map(d2n)

  val part = new Part("part", 0, Part.DEFAULT_CHANNEL)
  val phrase = new jm.music.data.Phrase(notes.toArray)
  part.addPhrase(phrase)

  val leftHand = accompany(phrase.getEndTime)
  part.addPhrase(leftHand)

  val score = new Score
  score.setTempo(120)
  score.addPart(part)

  Write.midi(score, fileName)
}

The result:

The other differences can be explained by better use of note durations and rests, better accompaniment, and rich timbre of a real instrument.

Making it Sound More Human

After consulting with a Friendly Neighbourhood Music Man who noted that currently the biggest problem with the generated melodies is the lack of any form of strong or weak beats I’ve decided to try implementing proper accenting notes.

Since the oroginal piece was performed in the classical style I’ve decided to accent the 1 and 3 beats (by setting the dynamic to FF and F respectively) and holding the notes longer on those beats. The code for generating the notes is a little longer than before:

def statefulDigitToNote(d: Digit, pos: Int): (Note, Int) = {
  val delta: Int = d match {
    case 0 => -1 
    case 1 => 0
    case 2 => 2
    case 3 => 4
    case 4 => 5
    case 5 => 7
    case 6 => 9
    case 7 => 11
    case 8 => 12
    case 9 => 14
  }

  val dissonanceClass: DissonanceClass = {
    d match {
      case 0 => /* B MINOR_SECOND   */ DissonanceClass.Dissontant
      case 1 => /* C UNISON         */ DissonanceClass.Consontant
      case 2 => /* D MAJOR_SECOND   */ DissonanceClass.Imperfect
      case 3 => /* E MAJOR_THIRD    */ DissonanceClass.Imperfect
      case 4 => /* F PERFECT_FOURTH */ DissonanceClass.Consontant
      case 5 => /* G PERFECT_FIFTH  */ DissonanceClass.Consontant
      case 6 => /* A MAJOR_SIXTH    */ DissonanceClass.Imperfect
      case 7 => /* B MAJOR_SIXTH    */ DissonanceClass.Dissontant
      case 8 => /* C OCTAVE         */ DissonanceClass.Consontant
      case 9 => /* D OCTAVE+M2      */ DissonanceClass.Imperfect
    }
  }

  val (duration, dynamic) = if (pos % 16 == 0) {
    // first beat
    (4, Volumes.FF)
  } else if (pos % 16 == 8) {
    // third beat
    val dur = dissonanceClass match {
      case DissonanceClass.Consontant => 
        4
      case DissonanceClass.Imperfect  => 
        2
      case DissonanceClass.Dissontant => 
        2
    }

    dur -> Volumes.F
  } else {
    // everything else 
    val dur = dissonanceClass match {
      case DissonanceClass.Consontant => 
        4
      case DissonanceClass.Imperfect  => 
        2
      case DissonanceClass.Dissontant => 
        1
    }

    dur -> Volumes.MF
  }

  val n: Int = delta + (60 + 12)

  def mkNote(d: Double) = {
    new Note(n, d, dynamic)
  }

  val note = duration match {
    case 1 =>
      mkNote(Durations.SIXTEENTH_NOTE)
    case 2 =>
      mkNote(Durations.EIGHTH_NOTE)
    case other =>
      mkNote(Durations.QUARTER_NOTE)
  }

  note -> (pos + d)
}

def renderDigitsWithAccompaniamentWithState(
    fileName: String,
    digits: List[Digit]): Unit = {
  val part = new Part("part", 0, Part.DEFAULT_CHANNEL)
  val phrase = new jm.music.data.Phrase()

  // foldLeft gets confused by `Digit` so we use recursion
  def go(list: List[Digit], state: Int): Unit = list match {
    case Nil =>
      ()
    case digit :: rest =>
      val (note, newState) = statefulDigitToNote(digit, state)
      phrase.addNote(note)
      go(rest, newState)
  }
  go(digits, 0)

  part.addPhrase(phrase)

  val leftHand = accompany(phrase.getEndTime)
  part.addPhrase(leftHand)

  val score = new Score
  score.setTempo(120)
  score.addPart(part)

  Write.midi(score, fileName)
}

But the result (especially of e) is really fun to hear:

Footnotes

https://www.maa.org/external_archive/devlin/LockhartsLament.pdf ↩
a.k.a poor man’s transcribing skills ↩
I found another possible interpretation using the harmonic minor scale on youtube ↩
simply by adding "com.explodingart" % "jmusic" % "1.6.4" to libraryDependencies ↩